Discos dos Segredos

Com dois pratos parabólicos de frente um para o outro, pode comunicar com outra pessoa a uma longa distância.

Componentes:

2 pratos parabólicos alinhados corretamente

Princípio de funcionamento:

O princípio de funcionamento baseia-se nas propriedades da parábola, uma forma que permite que quaisquer raios paralelos que atingem a sua superfície sejam refletidos todos para o mesmo ponto, o foco. Da mesma forma, quaisquer raios emitidos do foco seriam refletidos pela parábola e enviados paralelamente para longe dela.

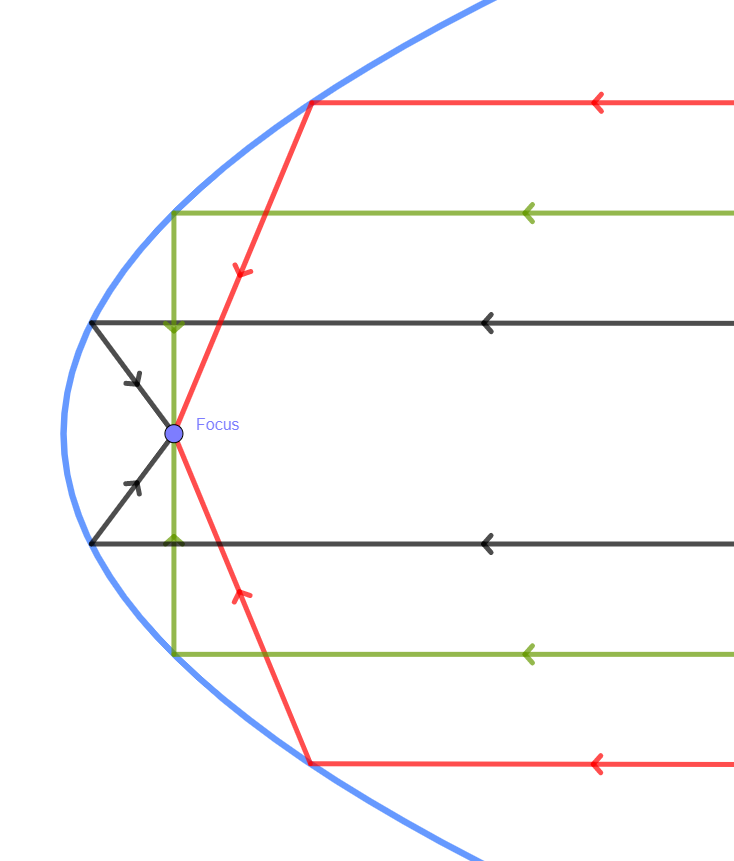
Se colocar o ouvido no ponto de foco, poderá ouvir claramente todos os sons coletados pelo prato. Se tiver um outro prato oposto a este e uma outra pessoa falando para o foco desse outro prato, poderá comunicar a longa distância apenas sussurrando.

Uma parábola refere-se a uma equação de uma curva, tal que um ponto na curva é equidistante de um ponto fixo – o ponto de foco e uma linha fixa – a diretriz. É importante notar que o ponto de foco não está na diretriz. A parábola é uma forma derivada de uma secção de um cone.

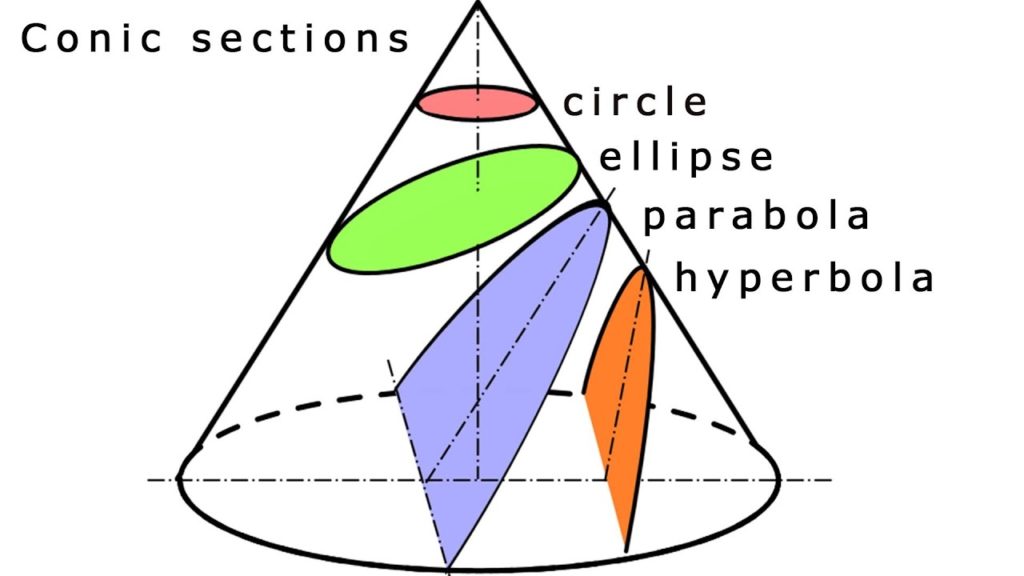
Equação da parábola

A equação geral de uma parábola é: y = a(x-h)² + k para uma parábola vertical (ou regular) ou x = a(y-k)² para uma horizontal (ou lateral), onde (h,k) denota o vértice. A equação padrão de uma parábola horizontal regular é y² = 4ax.

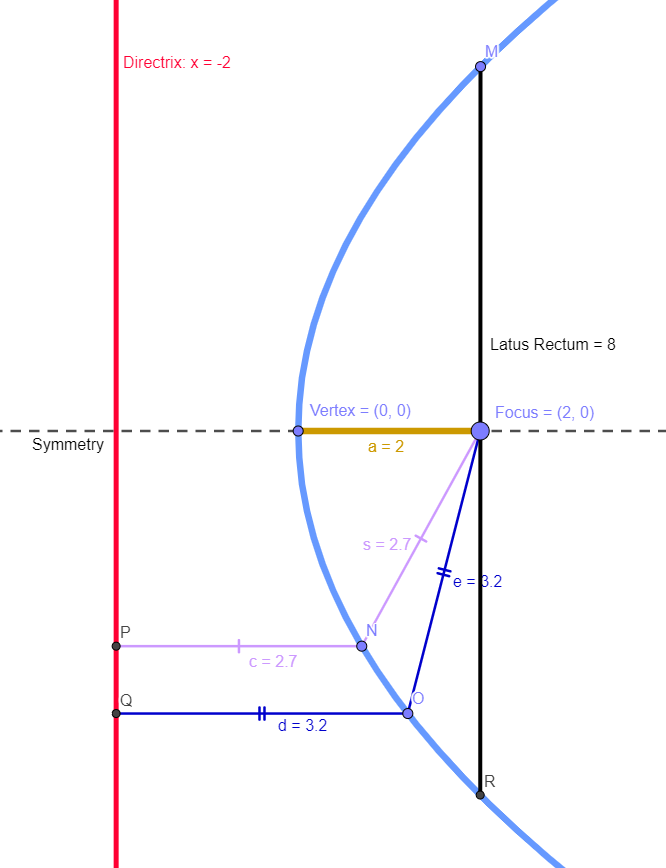
Alguns dos termos importantes abaixo são úteis para entender as características e partes de uma parábola.

Foco: O foco está na linha de simetria da parábola. O ponto (a, 0) é o foco da parábola acima.
Diretriz: A linha traçada paralela ao eixo y e passando pelo ponto (-a, 0) é a diretriz da parábola. A diretriz é perpendicular ao eixo da parábola.
Distância focal: A distância de um ponto (x1, y1) na parábola, a partir do foco, é a distância focal. A distância focal também é igual à distância perpendicular deste ponto à diretriz.
Latus Rectum: É a corda focal que é perpendicular ao eixo da parábola e passa pelo foco da parábola. O comprimento do latus rectum é igual a quatro vezes a distância focal.
Excentricidade: (e = 1). É a razão entre a distância de um ponto ao foco e a distância do ponto à diretriz. A excentricidade de uma parábola é igual a 1.
Vértice: é o ponto na interseção da parábola e a linha de simetria.

Instruções:

Sussurre no centro deste prato parabólico e a outra pessoa que estiver ouvindo no foco do outro prato parabólico conseguirá ouvi-lo(a) claramente. Tente se comunicar nos dois sentidos.

Links:

https://mathbitsnotebook.com/Geometry/Equations/EQParabola.html

https://www.pbs.org/wgbh/nova/teachers/activities/3406_solar_03.html