Whisper Dish

With two parabolic dishes facing each other you can communicate with someone else from a long distance apart.

Components:

2 parabolic dishes correctly aligned

Working Principle:

The working principle relies on the properties of the parabola, a shape that allows any parallel rays that hit its surface to be reflected all to the same point, the focus point. Similarly any rays emitted from the focus would be reflected by the parabola and sent across parallel away from it.

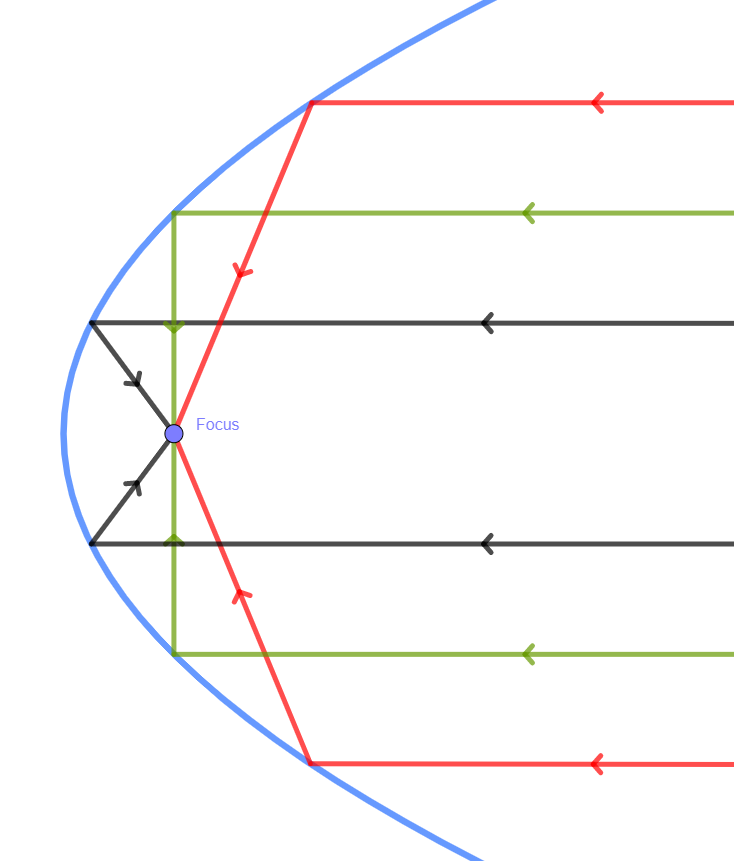
If you place your ear at the focus point you’ll be able to hear clearly all the sounds that are collected by the dish. If you have a second dish opposing with this one and a second person talking to the focus point of that other dish then you should be able to communicate at a long distance just by whispering.

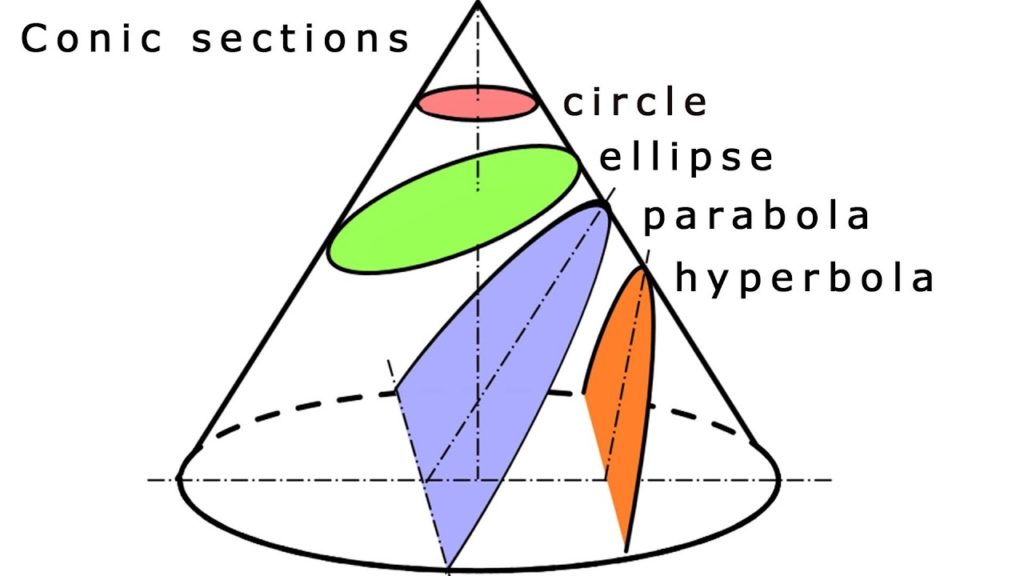
A parabola refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point – the focus point, and a fixed line – the directrix. It’s important to note that the focus point does not lie on the directrix. The parabola is a shape derived from a section of a cone.

Parabola Equation

The general equation of a parabola is: y = a(x-h)² + k for a vertical (or regular) parabola or x = a(y-k)² +h for a horizontal (or sideways) one, where (h,k) denotes the vertex. The standard equation of a regular horizontal parabola is y² = 4ax.

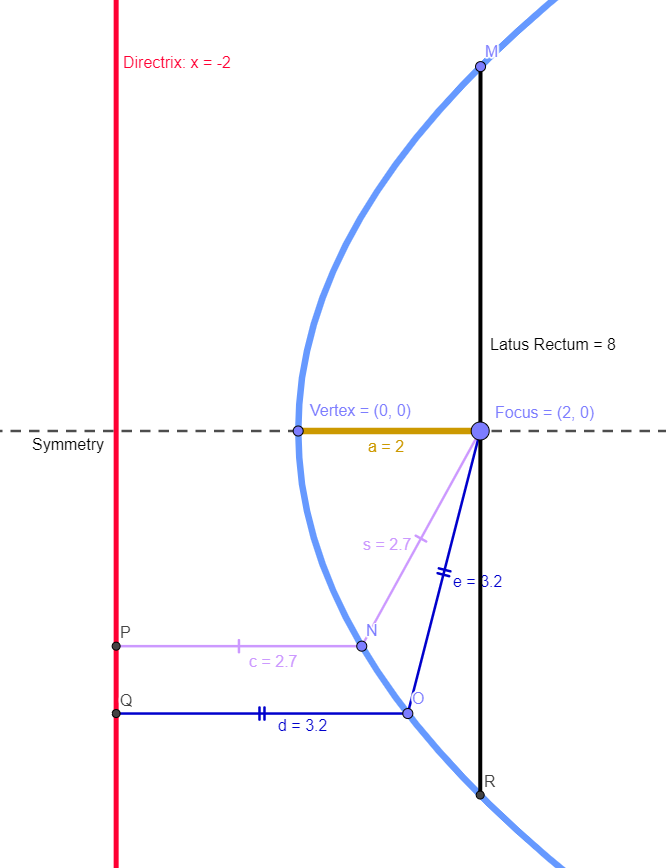
Some of the important terms below are helpful to understand the features and parts of a parabola.

Focus: The focus lies on the line of symmetry of the parabola. The point (a, 0) is the focus of the parabola above.
Directrix: The line drawn parallel to the y-axis and passing through the point (-a, 0) is the directrix of the parabola. The directrix is perpendicular to the axis of the parabola.
Focal Distance: The distance of a point (x1, y1) on the parabola, from the focus, is the focal distance. The focal distance is also equal to the perpendicular distance of this point from the directrix.
Latus Rectum: It is the focal chord that is perpendicular to the axis of the parabola and is passing through the focus of the parabola. The length of the latus rectum is equal to four times the focal length.
Eccentricity: (e = 1). It is the ratio of the distance of a point from the focus, to the distance of the point from the directrix. The eccentricity of a parabola is equal to 1.
Vertex: is the point at the intersection of the parabola and its line of symmetry.

Instructions:

Whisper at the centre of this parabolic dish and your friend listening at the centre of the other parabolic dish will hear you clearly. Try to communicate both ways.

Links:

https://mathbitsnotebook.com/Geometry/Equations/EQParabola.html

https://www.pbs.org/wgbh/nova/teachers/activities/3406_solar_03.html